Interface elements have to be used with material models describing the constitutive behavior of interfaces between two materials (e.g. between steel reinforcement and concrete), or between two bodies in contact. Such interface laws are formulated in terms of the traction vector t and the displacement jump vector δ.
A simple interface material with generally different stiffness in compression, tension and shear. It is intended for simulating a contact with low stiffness in tension and high in compression. The parameter transitionOpening specifies initial gap embedded in an element which causes transition from tension to compression. For example, transitionOpening=0.01 m means that there exists the embedded gap which needs displacement jump 0.01 m to close. Traction-separation law for normal direction takes the following form:
where smoothMag controlls smoothing magnitude. Tangential stiffness for normal direction is found by differentiating Eq. (253)
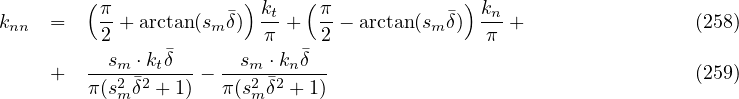
Shear stiffness remains constant during all possible loadins and there is no influence of normal direction.
| Description | Cohesive interface material |
| Record Format | cohInt (in) # kn(rn) # ks(rn) # [ stiffCoeffKn(rn) #] [ smoothMag(rn) #] [ transitionOpening(rn) #] |
| Parameters | - material number |
| - kn (penalty) stiffness in compression |
|
| - ks stiffness in shear |
|
| - stiffCoeffKn ratio (tensile stiffness / compression stiffness) |
|
| - smoothMag smoothing parameter for transition between tensile/compressive behavior |
|
| - transitionOpening embedded gap in the element |
|
| Supported modes | _1dInterface,_2dInterface,_3dInterface |
This model is described in Section 1.5.9.
This model provides a simple interface law with penalty-type contact and friction. In the normal direction, the response is linear elastic, but with different stiffnesses in tension and in compression (stiffness kn in compression, kn*stiffcoeff in tension). By setting kn to a high value, the penetration (overlap) can be reduced, in the sense of the penalty approach. By setting stiffcoeff to 0, free opening of the gap can be allowed.
The shear response is elastoplastic, with the yield limit dependent on the normal traction. Crosssection’s width, height or area have no influence on the results. The magnitude of the shear traction σT must not exceed the yield limit computed according to a Coulomb-like friction law as the product of the (negative part of) normal traction σN and a dimensionless coefficient of friction fc:
| (260) |
σN is computed multiplying a known normal strain and a known stiffness in tension or in compression.
If regularized is set to true, the regularized version of the model is used. The regularization parameter m allows to controll, how close to original formulation the regularized model is. The defaukt value is 15, the higher value the closer resposes are. The regularized version has following form:
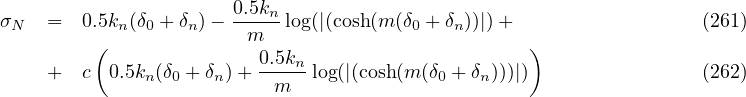
where c is ratio of tensile/compressive stiffness (stiffcoeff), δ0 normal clearance, δn normal strain (jump), and m denoting the regularization coefficient. Consistent tangent stiffness is computed by differentiating the above relation.
The shear elastic stiffness is assumed to be kn (i.e., equal to the normal stiffness). If the normal traction is tensile or zero, no shear traction can be transmitted by the interface. In the future, this law will be enriched by a cohesion-like term.
If used in connection of two nodes with interface1delement, the element-level parameter normal determines what is compression and what is tension (from the 1st node to the 2nd node in normal direction it is tension). If normalClearance is defined, the element has tensile stiffness until the gap within the element is closed. This feature allows simulating two faces with a gap. When the gap is smaller than normalClearance, the element stiffness changes to compression, see Figure 12.
The model description and parameters are summarized in Tab. 54.
| Description | Simple interface material |
| Record Format | simpleintermat (in) # kn(rn) # [ fc(rn) #] [ stiffcoeff(rn) #] [ normalClearance(rn) #] |
| Parameters | - material number |
| - kn (penalty) stiffness in compression |
|
| - fc friction coefficient |
|
| - stiffcoeff ratio (tensile stiffness / compression stiffness) |
|
| - normalClearance free distance within element |
|
| - regularized when true use regularized formulation (Default is False) |
|
| - m regularization coefficient m (default value is 15) |
|
| Supported modes | _1dInterface |
The complex steel/concrete interaction can be modelled with a bond-slip relation, which describes the bond stress (tangential interface traction), τ, in terms of the relative reinforcement slip (tangential interface jump), s. This interface material model is based on the local bond–slip relationship for reinforced concrete under good bond conditions outlined in the the fib Model Code for Concrete Structures 2010 [32]. In general, the model is formulated in terms of the interface traction vector t and the interface jump vector δ. In the model, the interface is assumed to have only elastic stiffness kn in the normal direction. The normal interface traction is then evaluated elastically from the normal interface jump, i.e. tn = knδn. The tangential traction tt = τ is evaluated from the user-specified function τ(s), see Figure 13:
| (263) |
For an exponent α smaller than 1 (default value 0.4), the initial tangential stiffness of the interface, ks, is undefined
and cannot be used in numerical computations. Therefore, this stiffness needs to be specified manually.
Should the provided stiffness be smaller than kn =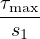 
, it will be automatically adjusted to this value.
Note that only elastic tangent stiffness is supported. Hence, in 2D the tangent stiffness matrix takes the
form
| (264) |
Model description and the input parameters are summarized in Tab. 55.
| Description | Bond-slip model for reinforced concrete |
| Record Format | bondceb (in) # kn(rn) # ks(rn) # s1(rn) # s2(rn) # s3(rn) # taumax(rn) # [ tauf(rn) #] [ alpha(rn) #] |
| Parameters | - material number |
| - kn interface elastic normal stiffness |
|
| - ks interface elastic tangential (shear) stiffness |
|
| - s1 characteristic slip value |
|
| - s2 characteristic slip value |
|
| - s3 characteristic slip value |
|
| - taumax maximum bond stress |
|
| - tauf residual bond stress at reinforcement pull-out |
|
| - alpha bond-slip curve parameter (exponent) |
|
| Supported modes | _2dInterface, _3dInterface |
![⌊ ⌋
∂tn ∂tn [ ]
-∂t= |⌈ ∂δn ∂s |⌉ = kn 0
∂ δ ∂τ- ∂-τ 0 ks
∂δn ∂s](matlibmanual323x.png)
