Weak form

By following the method of weighted residuals, we multiply the governing differential equations 1.4 in residual form by a sutable test functions $\delta$$u$, satisfying the homogeneous boundary conditions on $\Gamma_u$

$$\int_\Omega \delta$$$u$$$\cdot \left( \nabla \cdot\mbox{\boldmath $\sigma$} + F \right)\ d\Omega = \mbox{\boldmath $0$}$$

By applying the Green's formula, we arrive at

$$\int_\Omega\nabla \delta$$$u$$$\cdot$$$\sigma$$$\ d\Omega = \int_\Omega\delta$$$u$$$\cdot$$$F$$$\ d\Omega + \int_\Gamma\delta$$$u$$$\cdot$$$\sigma$$n$$$\ d\Gamma$$

Then we can substitute for the stresses and tractions and taking into account the symmetry of stress tensor ( $\sigma=C$ $\varepsilon$$)$

$$\int_\Omega\nabla ^s\delta \mbox{\boldmath$u$} \cdot \mbox{\boldmath$C$} \mbox{\boldmath$\varepsilon $} \ d\Omega = \int_\Omega\delta \mbox{\boldmath$u$} \cdot \mbox{\boldmath$F$} \ d\Omega + \int_\Gamma\delta \mbox{\boldmath$u$} \cdot \mbox{\boldmath$t$} \ d\Gamma$$ (1.5)

Or, equaivalently using Voight's notation

$$\int_\Omega\delta\tilde{\varepsilon }^T\tilde{\mbox{\boldmath$D$}... ...}\ d\Omega + \int_\Gamma\delta\mbox{\boldmath$u$}^T\mbox{\boldmath$t$}\ d\Gamma$$ (1.6)

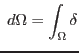
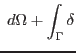
Note: this is equaivalent to the principle of virtual displacements. For hyperelastic material, the weak form is identical to the principle of minimum potential energy.