Equlibrium equations

Stress is defined as the force across a "small" boundary per unit area of that boundary, for all orientations of the boundary. In the most general case, called triaxial stress, the stress is nonzero across every surface element. Cauchy observed that the stress vector 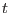$t$ across a surface is a linear function of the surface's normal vector $n$:

   $t$$$(x)=$$$\sigma$$$(x)$$$n$$$(x)$$

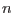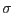
where 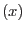$\sigma$$(x)$ is called the (Cauchy) stress tensor, completely describing the stress state at any point.

Figure 1.2: Balance between tractions and stresses in 2D

The components of the Cauchy stress tensor at every point in a material satisfy the equilibrium equations (Cauchy’s equlibrium equations). From the conservation of angular momentum follows the symmetry of the stress tensor. Therefore, the stress state of the medium at any point and instant can be specified by only six independent parameters, rather than nine. These may be written

$$\left[ \begin{array}{ccc} \sigma_{xx} & \tau_{xy} & \tau_{xz}\\... ..._{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{array}\right]$$

where the elements 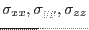$\sigma_{xx}, \sigma_{yy}, \sigma_{zz}$ are called the normal stresses (relative to the chosen coordinate system), and 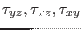$\tau_{yz}, \tau_{xz}, \tau_{xy}$ the shear stresses.

In a static equlibrium, the Cauchy stress components in every material point satisfy the equilibrium equations, see reffig:stressbalance

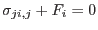$$\sigma_{ji, j} + F_i = 0$$ (1.3)

where we use summation convention over repated indices and 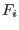$F_i$ are the components of the body force. In a compact tensorial notation we can write the above equation as

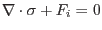$$\nabla \cdot\sigma + F_i = 0$$ (1.4)

Figure 1.3: Stress balance in 2D