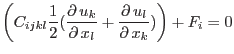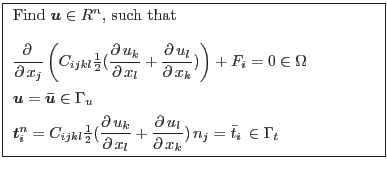Strong form

Starting from the equilibrium equations refeq:staticequlibrium3d, into which we can substitute the constituve equations and strain-displacement relation we obtain the equlibrium equation expressed in terms of displacements:

$\displaystyle \mbox{$\displaystyle\frac{\partial \,{}}{\partial \,{x_j}}$}$ $\displaystyle \left({C_{ijkl} {1\over 2}(\mbox{$\displaystyle\frac{\partial \,{... ...x{$\displaystyle\frac{\partial \,{u_l}}{\partial \,{x_k}}$})}\right) + F_i = 0$

This system of three partial differnetial equations can be solved, provided that appropriate boundary conditions are given. In summary, the strong form is the following:

$\fbox{ \begin{minipage}{8cm} Find $\mbox{\boldmath$u$}\in R^n$, such that\\ [4... ...l \,{u_l}}{\partial \,{x_k}}$})\,n_j = \bar t_i \,\in \Gamma_t$ \end{minipage}}$

Borek Patzak 2017-12-30