Let us consider discretization of the problem domain 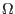 into set of nonoverlapping subdomains
into set of nonoverlapping subdomains 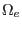 , called elements.
Next we will consider the approximation of the unknown displacement field, defined on individual subdomains. Note that the approximation is not arbitrary:
, called elements.
Next we will consider the approximation of the unknown displacement field, defined on individual subdomains. Note that the approximation is not arbitrary:
- The weak form kontains only first derivatives of the unknown and test functions, thus only
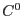 continuity is required.
continuity is required.
The element approxiamtion of the arbitrary function 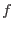 has the form
has the form
where 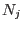 are so called shape or approximation functions and
are so called shape or approximation functions and 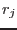 are nodal values.
Note that for the approximation functions to be interpolatory, the shape functions have to satisfy Kronecker-delta property, i.e.,
are nodal values.
Note that for the approximation functions to be interpolatory, the shape functions have to satisfy Kronecker-delta property, i.e.,
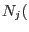
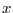
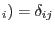 , where
, where
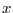
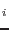 is the position vector of the i-th node. Also, the shape functions have to satisfy the condition
is the position vector of the i-th node. Also, the shape functions have to satisfy the condition
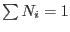 , which follows from the requirement to approximate the constant function.
The required continuity of element approximations have to be satisfied. This is typically achieved by enforcing the continuity at the nodal points.
In our case, the approximation of displacements and test functions is
, which follows from the requirement to approximate the constant function.
The required continuity of element approximations have to be satisfied. This is typically achieved by enforcing the continuity at the nodal points.
In our case, the approximation of displacements and test functions is
We will use the weak form 1.5, which using Voight's notation has the form
We will need also the derivatives of the displacement and test functions
where 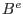 matrix contains the first partial derivatives of the shape functions.
By substiituting into the weak form 1.6 we obtain
matrix contains the first partial derivatives of the shape functions.
By substiituting into the weak form 1.6 we obtain
After introducing a mappig between element displacement vectors

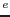 , nodal vectors of test function values
, nodal vectors of test function values
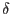
 and their global counterparts
and their global counterparts
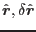 one can obtain
one can obtain
![$\displaystyle \delta\hat{\mbox{\boldmath$r$}}^{T} \left[ \hat{\mbox{\boldmath$K...
...$f$}}_\Omega - \hat{\mbox{\boldmath$f$}}_{\Gamma} \right] = \mbox{\boldmath$0$}$](img137.png) |
(1.12) |
By taking into account that the test fuctions are arbitrary (i.e.
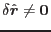 ), one finnaly obtains the following set of linear algebraic equations for unknonwn nodal displacements
), one finnaly obtains the following set of linear algebraic equations for unknonwn nodal displacements
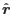 :
:
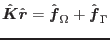 |
(1.13) |
Borek Patzak
2017-12-30
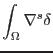
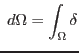
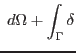
![$\displaystyle ^{e,T} \left[ \underbrace{\int_{\Omega^e} \mbox{\boldmath$B$}^{e,...
...ath$t$}}\ d\Gamma}_{\mbox{\boldmath$f$}^e_\Gamma} \right] = \mbox{\boldmath$0$}$](img135.png)
![]()
![]() , nodal vectors of test function values
, nodal vectors of test function values
![]()
![]() and their global counterparts
and their global counterparts
![]() one can obtain
one can obtain