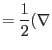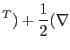Let us consider a deformable body as a collection of points, where position of each point is denoted as
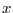
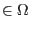 . In a deformed configuration the position of each point is identified by its position vector
. In a deformed configuration the position of each point is identified by its position vector
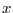
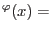
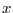
 . The displacement vector is then defined as:
. The displacement vector is then defined as:
Let us now examine the position in a local neighborhood of a point. The deformed position of such neighbor point with coordinates
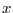
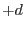
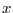 (where d
(where d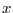 is infinitisemally small vector) is
is infinitisemally small vector) is
,
where
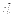
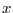
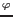 is the mapping of vector
is the mapping of vector
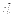
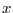 onto deformed configuration, see Fig. 1.2.1.
onto deformed configuration, see Fig. 1.2.1.
Figure 1.1:
Deformed configuration
|
|
Taking into account the definition of displacement vector 1.1 and using Taylor formula we get
where

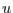
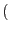
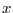
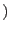 is the displacement gradient tensor (in small strain theory we assume
is the displacement gradient tensor (in small strain theory we assume
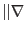
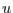
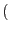
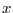
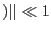 ).
The displacement gradient tensor can be decomposed into symetric and antisymmetric parts
).
The displacement gradient tensor can be decomposed into symetric and antisymmetric parts
The antisymmetric part corresponds to infinitesimal rotation. The symmeric part of displacement gradient tensor is therefore the measure of infinitesimal deformation
Borek Patzak
2017-12-30
![]()
![]()
![]() (where d
(where d![]() is infinitisemally small vector) is
is infinitisemally small vector) is