In this section we present the constituve relations (i.e. relations between stress and strain tensors) for the case of hyperelasticity, which could be defined in terms of strain energy density
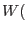
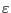
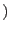 , which allows to evaluate stress components as partial derivatives:
, which allows to evaluate stress components as partial derivatives:
For example, the Hooke's law is defined using following strain energy potential
where
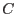 is forth order elasticity tensor. The equality of mixed derivatives
is forth order elasticity tensor. The equality of mixed derivatives
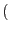

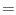

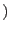 and symmetry of stress and strain tensors
and symmetry of stress and strain tensors
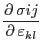
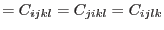 imply that there is in general maximum 21 independ components of the elasticity tensor.
In the simplest case, the elasticity tensor for isotropic linear elastic material can be described by only two parameters: either Lameś parameters (
imply that there is in general maximum 21 independ components of the elasticity tensor.
In the simplest case, the elasticity tensor for isotropic linear elastic material can be described by only two parameters: either Lameś parameters (
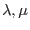 ) or more usual parametrs being Young's modulus
) or more usual parametrs being Young's modulus 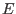 and Poisson's ratio
and Poisson's ratio 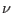 :
:
Borek Patzak
2017-12-30


![$\displaystyle C_{ijkl}=\lambda\delta_{ij}\delta_{kl}+2\mu {1\over 2}[\delta_{ik}\delta_{jl}+
\delta_{il}\delta_{jk}] \equiv$](img82.png)