Differentiation of the elastic stress-strain relations (4.8) and the discrete flow rule (4.9) yields
Combining this two equations, one obtains following relation
where

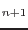 is the algorithmic moduli defined as
is the algorithmic moduli defined as
 ![$\displaystyle _{n+1}=\left[\mbox{\boldmath$D$}^{-1}+\sum\lambda^i\partial_{\sig...
...\lambda\partial_{\sigma\kappa}g\partial_{\sigma}\mbox{\boldmath$\kappa$}\right]$](img503.png) |
(4.27) |
Differentiation of discrete consistency condition yields
By substitution of (4.26) into (4.28) the following relation is obtained
where matrix
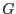 is defined as
is defined as
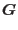 ![$\displaystyle =\left[\mbox{\boldmath$V$}^T\mbox{\boldmath$\Xi$}\mbox{\boldmath$...
...kappa}\mbox{\boldmath$f$}\partial_{\lambda}\mbox{\boldmath$\kappa$}\right]^{-1}$](img510.png) |
(4.30) |
Finally, by substitution of (4.30) into (4.26) one obtains the algorithmic elastoplastic tangent moduli
Borek Patzak
2017-12-30