Let us assume, that at time 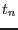 the total and plastic strain vectors and internal variables are known
the total and plastic strain vectors and internal variables are known
By applying an implicit backward Euler difference scheme to the evolution equations (4.2 and 4.4)
and making use of the initial conditions the following discrete non-linear system is obtained
In addition, the discrete counterpart of the Kuhn-Tucker conditions becomes
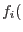 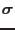 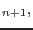 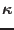 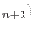 |
 |
0 |
(4.10) |
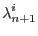 |
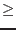 |
0 |
(4.11) |
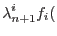 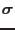 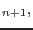 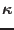 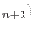 |
 |
0 |
(4.12) |
In the standard displacement-based finite element analysis, the strain evolution is determined by the displacement increments computed on the structural level. The basic task on the level of a material point is to evaluate the stress evolution generated by strain history.
According to this, the strain driven algorithm is assumed, i.e. that the total strain
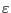
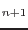 is given.
Then, the Kuhn-Tucker conditions determine whether a constraint is active. The set of active constraints is denoted as
is given.
Then, the Kuhn-Tucker conditions determine whether a constraint is active. The set of active constraints is denoted as 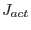 and is defined as
and is defined as
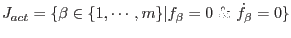 |
(4.13) |
Let's start with the definition of the residual of plastic flow
By noting that total strain
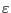
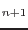 is fixed during the increment we can express the plastic strain increment using (4.2) as
is fixed during the increment we can express the plastic strain increment using (4.2) as
The linearization of the plastic flow residual (4.14) yields4.1
From the previous equation, the stress increment
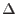
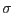 can be expressed as
can be expressed as
where
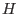 is algorithmic moduli defined as
is algorithmic moduli defined as
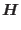 ![$\displaystyle =\left[\mbox{\boldmath$D$}^{-1}+\sum\lambda\partial_{\sigma\sigma}g+\sum\lambda\partial_{\sigma\kappa}g\partial_{\sigma}\kappa\right]$](img470.png) |
(4.18) |
Differentiation of active discrete consistency conditions (4.10) yields
Finally, by combining equations (4.17) and (4.19), one can obtain expression for incremental vector of consistency parameters
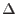
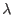
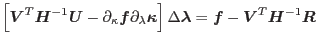 |
(4.20) |
where the matrices
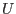 and
and
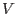 are defined as
are defined as
Before presenting the final return mapping algorithm, the algorithm for determination of the active constrains should be discussed. A yield surface 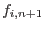 is active if
is active if
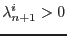 . A systematic enforcement of the discrete Kuhn-Tucker condition (4.10), which relies on the solution of return mapping algorithm, then serves as the basis for determining the active constraints. The starting point in enforcing (4.10) is to define the trial set
. A systematic enforcement of the discrete Kuhn-Tucker condition (4.10), which relies on the solution of return mapping algorithm, then serves as the basis for determining the active constraints. The starting point in enforcing (4.10) is to define the trial set
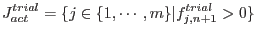 |
(4.23) |
where
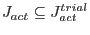 . Two different procedures can be adopted to determine the final set
. Two different procedures can be adopted to determine the final set 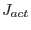 . The conceptual procedure is as follows
. The conceptual procedure is as follows
- Solve the closest point projection with
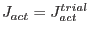 to obtain final stresses, along with
to obtain final stresses, along with
 .
.
- Check the sign of
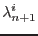 . If
. If
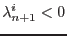 , for some
, for some
 , drop the
, drop the 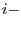 th constrain from the active set and goto first point. Otherwise exit.
th constrain from the active set and goto first point. Otherwise exit.
In the procedure 2, the working set
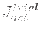 is allowed to change within the iteration process, as follows
is allowed to change within the iteration process, as follows
- Let
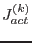 be the working set at the k-th iteration. Compute increments
be the working set at the k-th iteration. Compute increments
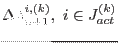 .
.
- Update and check the signs of
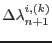 . If
. If
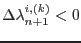 , drop the i-th constrain from the active set
, drop the i-th constrain from the active set
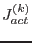 and restart the iteration. Otherwise continue with next iteration.
and restart the iteration. Otherwise continue with next iteration.
If the consistency parameters
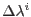 can be shown to increase monotonically within the return mapping algorithm, the the latter procedure is preferred since it leads to more efficient computer implementation.
can be shown to increase monotonically within the return mapping algorithm, the the latter procedure is preferred since it leads to more efficient computer implementation.
The overall algorithm is convergent, first order accurate and unconditionally stable.
The general algorithm is summarized in Tab. 4.2.2.
Table 4.1:
General multisurface closest point algorithm
![\begin{table}{\small
\begin{enumerate}
\item
Elastic predictor
\par
\begin{enum...
...[(i)]
Set k=k+1 and goto step (b)
\end{enumerate}\end{enumerate}}\end{table}](img497.png) |
Borek Patzak
2017-12-30
![]() is active if
is active if
![]() . A systematic enforcement of the discrete Kuhn-Tucker condition (4.10), which relies on the solution of return mapping algorithm, then serves as the basis for determining the active constraints. The starting point in enforcing (4.10) is to define the trial set
. A systematic enforcement of the discrete Kuhn-Tucker condition (4.10), which relies on the solution of return mapping algorithm, then serves as the basis for determining the active constraints. The starting point in enforcing (4.10) is to define the trial set
![]() is allowed to change within the iteration process, as follows
is allowed to change within the iteration process, as follows