Let
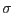
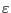
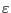
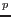 be the stress, total strain, and plastic strain vectors, respectively.
It is assumed that the total strain is decomposed into reversible elastic and irreversible plastic parts
be the stress, total strain, and plastic strain vectors, respectively.
It is assumed that the total strain is decomposed into reversible elastic and irreversible plastic parts
The elastic response is characterized in terms of elastic constitutive matrix
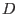 as
as
As long as the stress remains inside the elastic domain, the deformation process is purely elastic and the plastic strain does not change.
It is assumed that the elastic domain, denoted as 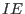 is bounded by a composite yield surface. It is defined as
is bounded by a composite yield surface. It is defined as
where
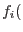
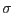
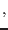
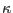
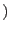 are
are 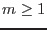 yield functions intersecting in a possibly non-smooth fashion. The
vector
yield functions intersecting in a possibly non-smooth fashion. The
vector
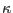 contains internal variables controlling the evolution of yield surfaces (amount of hardening or softening).
The evolution of plastic strain
contains internal variables controlling the evolution of yield surfaces (amount of hardening or softening).
The evolution of plastic strain
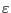
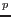 is expressed in Koiter's form. Assuming the non-associated plasticity, this reads
is expressed in Koiter's form. Assuming the non-associated plasticity, this reads
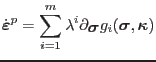 |
(4.4) |
where 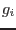 are plastic potential functions. The
are plastic potential functions. The 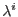 are referred as plastic consistency parameters, which satisfy the following Kuhn-Tucker conditions
are referred as plastic consistency parameters, which satisfy the following Kuhn-Tucker conditions
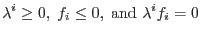 |
(4.5) |
These conditions imply that in the elastic regime the yield function must remain negative and the rate of the plastic multiplier is zero (plastic strain remains constant) while in the plastic regime the yield function must be equal to zero (stress remains on the surface) and the rate of the plastic multiplier is positive.
The evolution of vector of internal hardening/softening variables
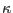 is expressed in terms of a general
hardening/softening law of the form
is expressed in terms of a general
hardening/softening law of the form
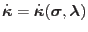 |
(4.6) |
where
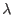 is the vector of plastic consistency parameters
is the vector of plastic consistency parameters 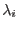 .
.
Borek Patzak
2017-12-30