For the time discretization of the momentum equation, a general trapezoid rule can be adopted. Using this rule, the time derivative of a generic function 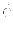 can be approximated by following equation
can be approximated by following equation
![$\displaystyle [\phi(x,t)]^{n+\theta} = \theta\phi(x,t^{n+1})+(1-\theta)\phi(x,t^n)=\theta\phi^{n+1}+(1-\theta)\phi^n\;.$](img338.png) |
(2.40) |
Rewriting the time derivative on the left hand side of the momentum balance (2.35) as a finite difference in time and applying the trapezoidal rule on the right hand side, we obtain
The parameter 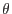 can take values from the interval
can take values from the interval ![$ [0,1]$](img341.png) . The approximation is considered as a weighted average of the derivative values in the time step
. The approximation is considered as a weighted average of the derivative values in the time step 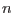 and
and 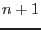 . Using a specific value of the
. Using a specific value of the 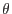 parameter, well-known methods can be recovered: The explicit Euler method
parameter, well-known methods can be recovered: The explicit Euler method 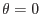 , the backward Euler for
, the backward Euler for 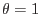 or the Crank-Nicolson method
or the Crank-Nicolson method
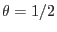 . The current implemantation of PFEM allows the use of explicit and backward (implicit) method.
. The current implemantation of PFEM allows the use of explicit and backward (implicit) method.
Borek Patzak
2017-12-30