Next: Spatial discretization Up: Transient incompressible flow - Previous: Time discretization Contents
![$\displaystyle \approx \frac{u^{n+1}_i-u^n_i}{\Delta t}=\frac{u^{n+1}_i-u^*_i+u^...
...ial x_j}\left(\frac{\partial u_i}{\partial x_j}\right)+b_i\right]^{n+\theta}\;.$](img346.png) |
(2.42) |
The pressure split is here introduced by the new parameter ![]() defining the amount of splitting and can take values from 0 to 1. The body loads are considered to be constant over time step.
defining the amount of splitting and can take values from 0 to 1. The body loads are considered to be constant over time step.
In a similar way, the fractional step method is applied on the mass conservation equation. Here, the time derivative of density would be approximated. As we examine an incompressible flow, whose density does not change in time, merely the intermediate velocity term is incorporated in the divergence of the velocity.
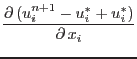 |
(2.45) |
By substituting for the velocity difference into the equation (2.44) we obtain
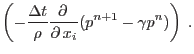 |
(2.48) |
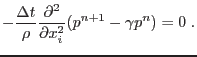 |
(2.49) |
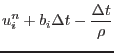 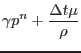 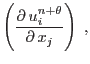 |
(2.50) | ||
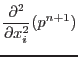 |
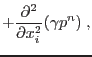 |
(2.51) | |
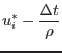 |
(2.52) |
The above PFEM formulation is based on the paper by Idelsohn, Oñate and Del Pin [#!Idelsohn04!#]. The authors described an approach using arbitrary time discretization scheme and pressure split factor. Their choice of implicit scheme
![]() was motivated by better convergence properties, whereas the decision for
was motivated by better convergence properties, whereas the decision for
![]() leading to greater pressure split was driven by better pressure stabilization.
leading to greater pressure split was driven by better pressure stabilization.