The Particle finite element method (PFEM) is based on the Lagrangian form of the Navier-Stokes equation for incompressible Newtonian fluids. Assuming the density does not change in time for an incompressible fluid, the continuity equation reduces to zero requirements for the divergence of the velocity. The Navier-Stokes equations take the form
For the deviatoric stress in Newtonian fluids a linear dependency of stress tensor and strain rate tensor is adopted and for the Newtonian fluids. Considering the incompressibility of the fluid, the Cauchy stress reads
This equation is known as Stokes' law and its Cartesian form writes
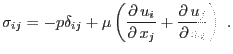 |
(2.33) |
Substituting the expression of Cauchy stress from Stokes' law (2.32) into the momentum equation (2.30) and rewriting gives
The governing equations of the mass (2.31) and momentum conservation (2.34) form can be written in the Cartesian form for the individual component 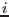 using Einstein summation convention
using Einstein summation convention
The equations are accompanied by a set of standard boundary conditions imposed on the complementary parts of the domain boundary
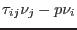 |
 |
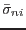 on on 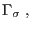 |
(2.37) |
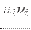 |
 |
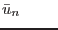 on on 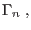 |
(2.38) |
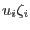 |
 |
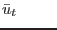 on on 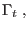 |
(2.39) |
where 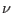 or
or 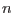 denotes the normal direction to the boundary and
denotes the normal direction to the boundary and 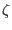 or
or 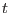 the tangential one. The bar sign over a quantity
the tangential one. The bar sign over a quantity 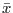 stands for its prescribed value.
stands for its prescribed value.
Borek Patzak
2017-12-30
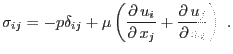
![]() using Einstein summation convention
using Einstein summation convention