Lattice transport elements have to be used with this material model. A positive sign is assumed for liquid tension,
unlike the convention of soil mechanics which assumes compression positive.
These transport elements are idealised as one-dimensional conductive pipes. The gradient of hydraulic head, which governs flow rate along each transport element, is determined from the capillary pressures Pc at the two nodes.
The mass balance equation describes the change in moisture inside a porous element as a consequence of liquid flow and solid-liquid retention. It leads to the following partial differential equation
| (303) |
where Pc is the capillary pressure, c is the mass capacity function(s2m-2), k is the Darcy hydraulic conductivity
(ms-1), ρ is the fluid mass density, g is the acceleration of gravity, z is the capillary height and t is the
time.
The hydraulic conductivity k consists of
| (304) |
where k0 is the hydraulic conductivity of the intact material and kc is the additional conductivity due to
cracking.
Darcy hydraulic conductivity k0 is defined as
| (305) |
where μ is the dynamic viscosity (Pa.s), κ is the permeability also called intrinsic conductivity(m2), and κr is the
relative conductivity. κr is a function of the effective degree of saturation.
The cracking part is
| (306) |
where ξ is a tortuosity factor taking into account the roughness of the crack surface, wc is the equivalent crack opening of the dual mechanical lattice and h is the length of the dual mechanical element.
The discrete form of the differential equation for mass transport for a one-dimensional transport element is
| (307) |
where Pc is a vector containing the nodal values of the capillary pressure, αe is the conductivity matrix, Ce is the
capacity matrix and fe is the nodal flow rate vector (kg.m3).
The capacity matrix is
| (308) |
where c is the capacity of the material, l is the length of the transport element and A is the cross-sectional area of the
transport element.
The conductivity matrix is defined as
| (309) |
The mass transport equation is based on the constitutive laws for the capacity c and the hydraulic conductivity
k.
The capacity c is defined as
| (310) |
where θ is the volumetric water content (θ =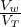 
with V w the volume of water, and V T the total volume) which is
calculated by a modified version of van Genuchten’s retention model. Note that the presence of a crack in an element
does not influence the capacity in the present model.
The volumetric water content is
| (311) |
where θr and θs are the residual and saturated water contents corresponding to effective saturation values of Se = 0
and Se = 1, respectively.
The effective degree of saturation Se is defined as
| (312) |
where θm is an additional model parameter and Pc(aev) is the air-entry value of capillary pressure which separates saturated (Pc < Pc(aev)) from unsaturated states (Pc ≥ Pc(aev)). It is intuitive that the smaller the pore size of the mate- rial, the larger the value of Pc(aev) will be.
The relative conductivity κr is a function of the effective degree of saturation and is defined as
| (313) |
If θm = θs, we have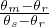 
= 1 : the equation reduces to the expression of the relative conductivity of the original van
Genuchten model.
The model parameters are summarized
| Description | Material for fluid transport in lattice models |
| Record Format | latticetransmat num(in) # d(rn) # k(rn) # vis(rn) # contype(in) # thetas(rn) # thetar(rn) # paev(rn) # m(rn) # a(rn) # thetam(rn) # [ ctor(rn) #] |
| Parameters | - num material model number |
| - d fluid mass density |
|
| - k permeability (m2) |
|
| - vis dynamic viscosity (Pa.s) |
|
| - contype unsaturated flow allowed when contype=1 |
|
| - thetas saturated water content |
|
| - thetar residual water content |
|
| - paev air-entry value of capillary pressure |
|
| - m van Genuchten parameter |
|
| - a van Genuchten parameter |
|
| - thetam additional model parameter for the modified version of van Genuchten’s retention model |
|
| - ctor coefficient of tortuosity (ctor = |
|
| Supported modes | 2dMassLatticeTransport |
![( [ ( )1-]m) 2
-Se-- m
∘ --|| 1 - 1- θmθs--θθrr- ||
κr = Se|| ---[----(------)1-]m||
( 1 - 1- --1-- m )
θmθs--θθrr-](matlibmanual367x.png)
