[next] [prev] [prev-tail] [tail] [up]

2.4 Nonlinear isotropic material for moisture transport – NlIsoMoisture

This is a more general model for nonlinear moisture transport in isotropic porous materials, based on a nonlinear sorption isotherm (relation between the pore relative humidity h and the water content w) and on a humidity-dependent moisture permeability. The governing differential equation solves water mass balance in a unit volume [kg/m3/s] and reads

k(h)∂h-= ∇ ⋅[c(h)∇h ]+ w dα- ∂t ndt
(275)

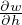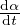where k(h) [kg/m3] is the humidity-dependent moisture capacity (k(h) = ∂w- ∂h which is derivative of the moisture content w(h) [kg/m3] with respect to the relative humidity), c(h) [kg/m/s] is the moisture permeability and the sink term wndα dt corresponds to non-evaporable water loss due to hydration. wn is non-evaporable water content for complete hydration per m3 [kg/m3] and α is degree of hydration [-]. For the majority of cements, 1 kg of cement consumes approximately 0.23 kg of non-evaporable water at complete hydration.

So far, six different functions for the sorption isotherm have been implemented (in fact, what matters for the model is not the isotherm itself but its derivative—the moisture capacity):

  1. Linear isotherm (isothermType = 0) is characterized only by its slope given by parameter capa. The isotherm can be shifted vertically, this is done by isooffset which has a meaning of moisture content at zero relative humidity.

  2. Piecewise linear isotherm (isothermType = 1) is defined by two arrays with the values of pore relative humidity iso_h and the corresponding values of moisture content iso_w(h). The arrays must be of the same size.

  3. Ricken isotherm [16] (isothermType = 2), which is widely used for sorption of porous building materials. It is expressed by the equation

    ln(1 - h) w(h) = w0 --------- d
    		(276)

    where w0 [kg/m3] is the water content at h = 0 and d [m3/kg] is an approximation coefficient. In the input record, only d must be specified (w0 is not needed). Note that for h = 1 this isotherm gives an infinite moisture content.

  4. Isotherm proposed by Kuenzel [16] (isothermType = 3) in the form

    (b--1)h w (h ) = wf b- h
    		(277)

    where wf [kg/m3] is the moisture content at free saturation and b is a dimensionless approximation factor greater than 1.

  5. Isotherm proposed by Hansen [14] (isothermType = 4) in the form

    ( ) ln-h-- 1∕n u(h) = uh 1 - A
    		(278)

    characterizes the amount of adsorbed water by the moisture ratio u [kg/kg]. To obtain the moisture content w, it is necessary to multiply the moisture ratio by the density of the solid phase. In (278), uh is the maximum hygroscopically bound water by adsorption, and A and n are constants obtained by fitting of experimental data.

  6. The BSB isotherm [4] (isothermType = 5) is an improved version of the famous BET isotherm. It is expressed in terms of the moisture ratio

    -------CkVmh--------- u(h) = (1- kh )(1+ (C - 1)kh)
    		(279)

    where V m is the monolayer capacity, and C depends on the absolute temperature T and on the difference between the heat of adsorption and condensation. Empirical formulae for estimation of the parameters can be found in [28]. Note that these formulae hold quite accurately for cement paste only; a reduction of the moisture ratio is necessary if the isotherm should be applied for concrete.

  7. Bilinear isotherm (isothermType = 6) is defined by its moisture capacity capa for relative humidity less than hx. Parameter wf defines moisture content at full saturation, h = 1. Convergence is substantially improved by a smooth transition on interval (hx - dx,hx + dx). Similarly to the linear isotherm the moisture content can be adjusted by parameter isooffset.

The present implementation covers three functions for moisture permeability:

  1. Piecewise linear permeability (permeabilityType = 0) is defined by two arrays with the values of pore relative humidity perm_h and the corresponding values of moisture content perm_c(h). The arrays must be of the same size.

  2. The Bažant-Najjar permeability function (permeabilityType = 1) is given by the same formula (274) as the diffusivity in Section 2.3. All parameters have a similar meaning as in (274) but c1 is now the moisture permeability at full saturation [kg/m⋅s].

  3. Permeability function proposed by Xi et al. [28] (permeabilityType = 2) reads

    [ γh(h-1)] c(h ) = αh + βh 1- 2-10
    		(280)

    where αh, βh and γh are parameters that can be evaluated using empirical mixture-based formulae presented in [28]. However, if those formulae are used outside the range of water-cement ratios for which they were calibrated, the permeability may become negative. Also the physical units are unclear.

Note that the Bajant-Najjar model from Section 2.3 can be obtained as a special case of the present model if permeabilityType is set to 1 and isothermType is set to 0. The ratio c1∕moistureCapacity then corresponds to the diffusivity parameter C1 from Eq. (273).

The model parameters are summarized in Tab. 69.

Description

Nonlinear isotropic material for moisture transport

Record Format

NlIsoMoistureMat num(in) # d(rn) # isothermType(in) # permeabilityType(in) # [ rhodry(rn) #] [ capa(rn) #] [ iso_h(ra) #] [ iso_w(h)(ra) #] [ dd(rn) #] [ wf(rn) #] [ b(rn) #] [ uh(rn) #] [ A(rn) #] [ nn(rn) #] [ c(rn) #] [ k(rn) #] [ Vm(rn) #] [ hx(rn) #] [ dx(rn) #] [ perm_h(ra) #] [ perm_c(h)(ra) #] [ c1(rn) #] [ n(rn) #] [ alpha0(rn) #] [ hc(rn) #] [ alphah(rn) #] [ betah(rn) #] [ gammah(rn) #] [ wn(rn) #] [ alpha(expr) #]

Parameters

- num material model number

- d material density

- isothermType isotherm function as listed above (0, 1, ...6)

- permeabilityType moisture permeability function as listed above (0, 1, 2)

- rhodry [kg/m3] density of dry material (for isothermType = 4 and 5)

- capa [kg/m3] moisture capacity (for isothermType = 0 and 6)

- isooffset [kg/m3] moisture capacity at zero relative humidity (for isothermType = 0 and 6)

- iso_h [-] humidity array (for isothermType = 1)

- iso_w(h) [kg/m3] moisture content array (for isothermType = 1)

- dd [-] parameter (for isothermType = 2)

- wf [kg/m3] is the moisture content at free saturation (for isothermType = 3 and 6)

- b [-] parameter (for isothermType = 3)

- uh [kg/kg] maximum hygroscopically bound water by adsorption (for isothermType = 4)

- A [-] parameter (for isothermType = 4)

- n [-] parameter (for isothermType = 4)

- Vm (for isothermType = 5)

- k (for isothermType = 5)

- C (for isothermType = 5)

- hx [-] transition relative humidity (for isothermType = 6)

- dx [-] length of the smooth transition (for isothermType = 6)

- perm_c(h) [kg m-1 s-1] moisture permeability array (for permeabilityType = 0)

- c1 [kg m-1 s-1] moisture permeability at full saturation (for permeabilityType = 1)

- n [-] exponent (for permeabilityType = 1)

- alpha0 [-] ratio between minimum and maximum diffusivity (for permeabilityType = 1)

- hc [-] relative humidity at which the diffusivity is exactly between its minimum and maximum value (for permeabilityType = 1)

- alphah [kg m-1 s-1] (for permeabilityType = 2)

- betah [kg m-1 s-1] (for permeabilityType = 2)

- gammah [-] (for permeabilityType = 2)

- wn [kg m-3] nonevaporable water content per m3 of concrete, default 0.23 kg/kg of cement

- alpha [-] function of degree of hydration

Supported modes

_2dHeat


Table 69: Nonlinear isotropic material for moisture transport - summary.

[next] [prev] [prev-tail] [front] [up]