Next: Transient incompressible flow - Up: Non-stationary nonlinear transport model Previous: Non-stationary nonlinear transport model Contents
Heat flow from a body surrounded by a medium at a temperature ![]() is governed by the Stefan-Boltzmann Law
is governed by the Stefan-Boltzmann Law
Alternatively (not implemented), a linearization using Taylor expansion around ![]() and neglecting higher-order terms results to
and neglecting higher-order terms results to
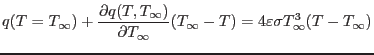 |
(2.28) |
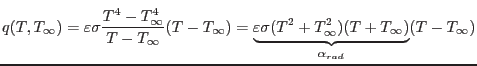 |
(2.29) |
Borek Patzak 2017-12-30