next up previous contents
Next: Newton-Raphson method Up: Solution procedures Previous: Solution procedures   Contents

Solution procedures for nonlinear systems

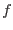
We illustrate this on problem of nonlinear mechanics. Our starting point is general form of equilibrium equations expressing the balance between internal 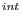$ f$$ ^{int}$ and external $ f$$ ^{ext}$

   $ f$$\displaystyle ^{int}($$ r$$\displaystyle ) =$   $ f$$\displaystyle ^{ext} $

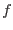
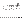
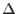
Suppose we are looking for an equilibrium at the end of load increment $ \Delta$$ f$$ ^{ext}$

$\displaystyle \mbox{\boldmath$f$}$$\displaystyle ^{int}($$\displaystyle \mbox{\boldmath$r$}$$\displaystyle +\Delta$$\displaystyle \mbox{\boldmath$r$}$$\displaystyle ) =$   $\displaystyle \mbox{\boldmath$f$}$$\displaystyle ^{ext}+\Delta$$\displaystyle \mbox{\boldmath$f$}$$\displaystyle ^{ext} $ (2.1)

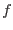
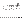
By the linearization of the nodal force vector around known equilibrium state we can obtain

$\displaystyle \mbox{\boldmath$f$}$$\displaystyle ^{int}($$\displaystyle \mbox{\boldmath$r$}$$\displaystyle )+$$\displaystyle \mbox{$\displaystyle\frac{\partial \,{\mbox{\boldmath$f$}^{int}}}{\partial \,{\mbox{\boldmath$r$}}}$}$$\displaystyle \Delta$$\displaystyle \mbox{\boldmath$r$}$$\displaystyle +O(\Vert\Delta$$\displaystyle \mbox{\boldmath$r$}$$\displaystyle \Vert^2)$ (2.2)

The derivative of internal force vector with respect to nodal displacements is called jacobian matrix and in solid mechanics as tangent stiffness matrix. For the case of material non-linearity

   $ f$$\displaystyle ^{e,int}($$ r^e$$\displaystyle )=\int_{\Omega^e}$$ B$$\displaystyle ^T$$ \sigma$$\displaystyle ($ $ \varepsilon $$\displaystyle ($$ r^e$$\displaystyle ))\ d\Omega \Rightarrow$   $\displaystyle \mbox{$\displaystyle\frac{\partial \,{\mbox{\boldmath $f$}^{e,int}}}{\partial \,{\mbox{\boldmath $d$}^e}}$}$$\displaystyle = \int_{\Omega^e}$$ B$$\displaystyle ^T$$\displaystyle \mbox{$\displaystyle\frac{\partial \,{\mbox{\boldmath $\sigma$}}}{\partial \,{\mbox{\boldmath $\varepsilon $}}}$}$$\displaystyle \mbox{$\displaystyle\frac{\partial \,{\mbox{\boldmath $\varepsilon $}}}{\partial \,{\mbox{\boldmath $r^e$}}}$}$$\displaystyle \ d\Omega = \int_{\Omega^e}$$ B$$\displaystyle ^T$$\displaystyle \mbox{$\displaystyle\frac{\partial \,{\mbox{\boldmath $\sigma$}}}{\partial \,{\mbox{\boldmath $\varepsilon $}}}$}$$ B$$\displaystyle {\mbox{\boldmath $r$}^e}\ d\Omega = \int_{\Omega^e}\mbox{\boldmath $B$}^T\mbox{\boldmath $D$}\mbox{\boldmath $B$}{\mbox{\boldmath $r$}^e}\ d\Omega $


Subsections
next up previous contents
Next: Newton-Raphson method Up: Solution procedures Previous: Solution procedures   Contents
Borek Patzak 2017-12-30