Many engineering problems initiate demands for large-scale computing, which must be feasible from the view of both time and available resources. The parallel processing allows not only obtaining results in acceptable time by significantly speeding up the analysis, but also performing large and complex analyses, which often do not fit into a single, even well equipped, machine with one processor unit (regardless of achieved speedup).

The design of parallel algorithms requires the partitioning of the problem into a set of tasks, the number of which is greater than or equal to the number of available processors. The partitioning of the problem can be fixed at runtime (static load balancing) or can change during the solution (dynamic load balancing).

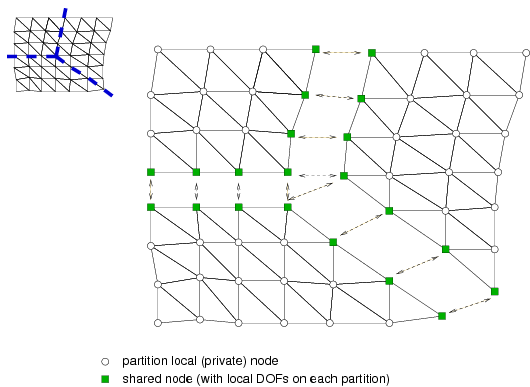
The adopted parallelization strategy in OOFEM is based on the mesh partitioning. Generally, two dual partitioning concepts for the parallelization of finite element codes exist. With respect to the character of a cut dividing the problem mesh into partitions, one can distinguish between node-cut and element-cut concepts.

In the presented study, the node-cut approach will be considered. This approach is based on a unique assignment of individual elements to partitions. A node is then either assigned to a partition (local node), if it is surrounded exclusively by elements assigned to that partition, or shared by several partitions (shared node), if it is incident to elements owned by different partitions

To be optimally load-balanced, the partitioning should take into account a number of factors, namely

• The computational work on each sub-domain should be balanced, so that no processor will be waiting for others to complete. The computational work is typically related to elements, and can be, for example, computed as a sum of individual element computational weights, which express the amount of numerical work (number of operations) associated with each element compared to the selected reference element. The overall computational work should be distributed among individual processors according to their relative performance.
• The interface between the partitions should be minimal, in order to reduce the communication requirements among partitions. When assembling the governing equations, the contribution from neighboring nodes/elements is often needed and the accumulation of remote contributions will incur communication. The cost of accessing remote memory is far higher than that of accessing local memory, therefore it is important to minimize the communication cost.

The parallel distributed memory programming model is relying on message passing, a form of communication based on sending and receiving messages. OOFEM is based on Message Passing Interface (MPI). High-level communication services were developed on the top of the message passing library. On the lower level, the CommunicationBuffer class is defined, providing services for sending/receiving receiver and packing/unpacking services. Message packing/unpacking} to form a continuous data stream that can be send in a single message, avoids fine-grained communication, due to overhead connected with sending small messages instead of a single one (latency issues).

To facilitate the mutual data exchange between sub-domains, the ProcessCommunicatorBuffer class is introduced. It maintains its send and receive buffers (instances of the CommunicationBuffer class) that are used to communicate with a remote sub-domain. The separate send and receive buffers are necessary in order to fully exploit the advantages of non-blocking communication of inter-partition communication with mutual data exchange. Such exchange typically involves data related to certain entities only (for example, located on inter-partition boundaries) and is repeated several times for each solution step. This leads to the introduction of the ProcessCommunicator class, which maintains the communication rank of a remote partition, communication maps and an instance of the ProcessCommunicatorBuffer class. Communication maps, which can be thought of as lists of entities (nodes, elements) that participate in the communication, are established according to the mesh partitioning prior to the actual analysis, separately for the send and receive operations. The corresponding local send and remote receive (and vice versa) maps must be uniquely ordered to guarantee the correctness of packing and unpacking operations. In general, the communication maps vary dynamically during the analysis to reflect the potential repartitioning. The ProcessCommunicator class provides high-level services for packing and unpacking relevant data. A general implementation of these operations has been obtained using call-back procedures, which pack and unpack the data according to the communication maps using the elementary services provided by the CommunicationBuffer class.

Efficient parallel algorithm requires that all steps in solution procedure are parallelized. In a typical problem this involves assembly of characteristic problem, its solution, and postprocessing. These steps are facilitated by the fact, that on each partition, OOFEM assigns unique local code numbers to the local nodes as well as to the shared nodes.

Provided that the partitioning of the problem is given, each processor can assemble its local contribution to the global characteristic equation. This part is pretty identical to serial assembly process and therefore allows to share this part between serial and parallel part of the algorithm. After finishing assembly of local contributions, it is necessary to exchange the contributions for shared nodes on the inter-partition boundaries. This is in general very complex task. Fortunately, OOFEM communication layer provides high level support for these tasks: It assembles send and receive communication maps for all partitions. The send map contains the shared node numbers, for which the exchange, in terms of sending the local contributions to a particular remote partition, is required, while the receive map contains the shared node numbers, for which the exchange, in terms of receiving the contributions from a particular remote partition, is required. The exchange process then consists in packing the local contributions according to the send map and sending them to the corresponding partitions, followed by receiving remote partitions contributions and unpacking their contributions according to the receive maps.

The user is required to provide following methods:

1. A packing method for wrapping the local contributions (for example load vector contributions) according to the send map into a communication buffer. Then these packed contributions are sent to the corresponding (remote) partitions, where they are received and unwrapped using unpack method according to the receive maps.
2. As packing/unpacking requires to provide a sufficient buffer length to accommodate the data, the buffer length has to be determined in advance using provided method. (When dynamic buffers are used, this is not required, but may induce a small performance footprint).

When assembling sparse matrices in parallel, no specific action is needed, provided that the suitable sparse matrix representation is used (SMT_PetscMtrx, for example).

Fist, we have to create an instance of ProblemCommunicator class , named communicator, that will set up communication maps, provide communication buffers, etc. It should be an attribute of class representing our problem. This instance is conveniently created and initialized in our problem initialization routine.

IRResultType
MyEngngModel :: initializeFrom(InputRecord *ir)
{
    // problem specific part here
 
    // initialize communicator if in parallel mode
#ifdef __PARALLEL_MODE
    // first create send and receive communication buffers, here we use fix-length
    // static buffers (CBT_static) (size needs to be determined)
    commBuff = new CommunicatorBuff(this->giveNumberOfProcesses(), CBT_static);
    // and create communicator, later we will se how to use it
    communicator = new ProblemCommunicator(this, commBuff, this->giveRank(),
                                           this->giveNumberOfProcesses(),
                                           ProblemCommMode__NODE_CUT);
 
#endif
}

Following method illustrates how the assembly method for vector (load vector) is changed to support parallel assembly. It uses communicator, an instance of ProblemCommunicator class, that provides a high level interface hiding all low-level communication. Note that the implementation will work for both serial and parallel modes.

void
MyEngngModel :: assembleLoadVector (FloatArray &loadVector,                                              
                                    Domain *sourceDomain, EquationID ut, TimeStep *tStep)
{
  EModelDefaultEquationNumbering en;
 
  // resize load vector first to accomodate all local entries
  loadVector.resize( sourceDomain->giveEngngModel()->giveNumberOfEquations(EID_MomentumBalance) );
  // prepare for assembly
  loadVector.zero();
 
  // assemble element part of load vector
  this->assembleVectorFromElements(loadVector, tStep, ut, ElementForceLoadVector,
	                           VM_Total, en, sourceDomain);
  // assemble nodal part
  this->assembleVectorFromDofManagers(loadVector, tStep, ut, NodalLoadVector, 
                                      VM_Total, en, sourceDomain);
 
#ifdef __PARALLEL_MODE
        // parallel section (compiles only when parallel support is configured)
        // pack all data, need to pass pointer to engngModel, local vector, and packing method
        // this will call pack method for each remote partition
        communicator->packAllData( ( StructuralEngngModel * ) this, 
                                    & loadVector, 
                                    & MyEngngModel :: packLoad );
 
        // send the packed data to remote partitions and receive their data
        communicator->initExchange(LoadExchangeTag);
 
        // unpack all received data, parameters: pointer to engngModel, local vector, and unpacking method
        communicator->unpackAllData( ( StructuralEngngModel * ) this, 
                                      & loadVector, 
                                      & StructuralEngngModel :: unpackLoad );
        // finish exchange
        communicator->finishExchange();
#endif
 
}

The following code illustrates the implementation of pack and unpack methods. The methods should have two parameters: a vector containing source/target data and ProcessCommunicator, that uniquely determines the remote partition, contains send/receive buffers and provides corresponding send/receive maps.

int
MyEngngModel :: packLoad(FloatArray *src, ProcessCommunicator &processComm)
{
    /** This method wraps the shared nodes entries of given vector into 
        communication buffer. The buffer is attribute of given ProcessCommunicator, that also
        uniquely determines the remote partition 
     */  
    int result = 1;
    int i, size;
    int j, ndofs, eqNum;
    Domain *domain = this->giveDomain(1);
    IntArray const *toSendMap = processComm.giveToSendMap();
    ProcessCommunicatorBuff *pcbuff = processComm.giveProcessCommunicatorBuff();
    DofManager *dman;
    Dof *jdof;
 
    size = toSendMap->giveSize();
    for ( i = 1; i <= size; i++ ) {  // loop over send map entries (shared nodes)
        dman = domain->giveDofManager( toSendMap->at(i) ); // give shared node
        ndofs = dman->giveNumberOfDofs();                  
        for ( j = 1; j <= ndofs; j++ ) {                   // loop over shared node DOF's
            jdof = dman->giveDof(j);
            if ( jdof->isPrimaryDof() && ( eqNum = jdof->__giveEquationNumber() ) ) {
                // if DOF is primary (not linked) and no BC applied (equation number assigned)
                // then pack its corresponding value in given vector to buffer
                result &= pcbuff->packDouble( src->at(eqNum) );
            }
        }
    }
 
    return result;
}
 
 
int
MyEngngModel :: unpackLoad(FloatArray *dest, ProcessCommunicator &processComm)
{
    /** This method unpacks the received shared nodes entries into given vector. 
        The receive buffer is attribute of given ProcessCommunicator, that also
        uniquely determines the remote partition sending the data. 
     */  
 
    int result = 1;
    int i, size;
    int j, ndofs, eqNum;
    Domain *domain = this->giveDomain(1);
    dofManagerParallelMode dofmanmode;
    IntArray const *toRecvMap = processComm.giveToRecvMap();
    ProcessCommunicatorBuff *pcbuff = processComm.giveProcessCommunicatorBuff();
    DofManager *dman;
    Dof *jdof;
    double value;
 
 
    size = toRecvMap->giveSize();
    for ( i = 1; i <= size; i++ ) {   // loop over receive map 
        dman = domain->giveDofManager( toRecvMap->at(i) ); // give corresponding shared node
        ndofs = dman->giveNumberOfDofs();
        dofmanmode = dman->giveParallelMode();
        for ( j = 1; j <= ndofs; j++ ) {                   // loop over shared node DOFs
            jdof = dman->giveDof(j);
            if ( jdof->isPrimaryDof() && ( eqNum = jdof->__giveEquationNumber() ) ) {
                // if DOF is primary (not linked) and no BC applied (equation number assigned)
                // then unpdate buffer value into corresponding vector value
                result &= pcbuff->unpackDouble(value);
                if ( dofmanmode == DofManager_shared ) {
                    // remote contribution is added to local one
                    dest->at(eqNum) += value;
                } else {
                    _error3( "unpackLoad: DofMamager %d[%d]: unknown parallel mode", dman->giveNumber(), dman->giveGlobalNumber() );
                }
            }
        }
    }
 
    return result;
}

Provided that the suitable sparse matrix representation is used (SMT_PetscMtrx, for example) and solver (ST_Petsc, for example), no modification to the sparse matrix assembly procedure and linear system solution is necessary. We can simply pass sparse matrix, local load vector, and solution vector to the solver and get results!

void
MyEngngModel :: solveYourselfAt(TimeStep *tStep) {
 
   // create components of characteristic equation
   stiffnessMatrix = CreateUsrDefSparseMtrx(sparseMtrxType);
   loadVector.resize(this->giveNumberOfEquations(EID_MomentumBalance));
   displacementVector.resize(this->giveNumberOfEquations(EID_MomentumBalance));
   loadVector.zero(); displacementVector.zero();
 
   // initialize profile of stiffness matrix
   stiffnessMatrix->buildInternalStructure(this, di, EID_MomentumBalance, EModelDefaultEquationNumbering());
 
   // assemble stiffness and load vector
   stiffnessMatrix->zero(); // zero stiffness matrix
   this->assemble( stiffnessMatrix, tStep, EID_MomentumBalance, ElasticStiffnessMatrix,
                   EModelDefaultEquationNumbering(), this->giveDomain(di) );
   this->assembleLoadVector (loadVector,this->giveDomain(di),
                             EID_MomentumBalance, tStep);                                 
 
   // get numerical method to solve the problem
   this->giveNumericalMethod(tStep);
   // solve the problem (yes, this solves linear system in parallel!)
   nMethod->solve(stiffnessMatrix, & loadVector, & displacementVector);
   // postprocess results update nodes, elements, compute strains, stresses, etc
   this->updateYourself( this->giveCurrentStep() );
   // and we are done!
}

• B. Patzák and D. Rypl. Parallel adaptive finite element computations with dynamic load balancing. In B. H. V. Topping, L. F. Costa Neves, and R. C. Barros, editors, Proceedings of the Twelfth International Conference on Civil, Structural and Environmental Engineering Computing, Stirlingshire, United Kingdom, 2009. Civil-Comp Press. paper 114.
• B. Patzák and D. Rypl. A framework for parallel adaptive finite element computations with dynamic load balancing. In B. H. V. Topping, editor, CD-ROM Proceedings of the First International Conference on Parallel, Distributed and Grid Computing for Engineering, Pecs, Hungary, 2009. Civil-Comp Press. ISSN: 1759-3433, ISBN: 978-1-905088-29-4.
• B. Patzak,D. Rypl, and Z. Bittnar: Parallel explicit finite element dynamics with nonlocal constitutive models, Computers and Structures, 79 (26-28), 2287-2297, 2001.