Model for relaxation of prestressing steel - SteelRelaxMat

This section describes the implementation of the material model for steel relaxation given in Eurocode 2 (the same as in Model Code 2010) and in Bazant and Yu (J. of Eng. Mech, 2013) which reduces to the first model under constant strain. At variable strain history the first model uses the approach employing the so-called equivalent time approach described in Annex D in the Eurocode 2.

The current implementation takes into account only prestress losses due to steel relaxation, other losses (e.g. slip at anchorage, thermal dilation, friction, etc.) need to be treated separately. The same holds for the stress transfer from prestressing reinforcement to concrete in the region called transmission length. On the other hand, losses due to sequential prestressing, elastic deformation and both short-time and long-time creep and shrinkage are taken into account automatically provided that a suitable material model is chosen for concrete.

In the first approach the stress on the end of the time step is explicitly given by the current stress, prestressing level and the cumulative value of prestress losses. On the other hand, in Bazant's approach it is necessary to iterate on the material point level in order to reach equilibrium.

As a simplification the stress-strain diagram is in the current implementation assumed to be linear (no yielding), this should be sufficient for most cases.

Under a constant strain, the evolution of prestress loss is defined as

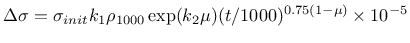$$\Delta \sigma = \sigma_{init} k_1 \rho_{1000} \exp(k_2 \mu) (t/1000)^{0.75(1-\mu)} \times 10^{-5}$$ (234)

where $\sigma_{init}$ is the initial value of prestress reduced for losses during prestressing, $t$ is time after prestressing in hours, $\mu = \sigma_{init} / f_{pk}$, $f_{pk}$ is the characteristic strength of prestressing steel in tension, and finally $k_1$, $k_2$, and $\rho_{1000}$ are material parameters determined by the relaxation properties of the reinforcement. For wires or cables with normal relaxation (class 1) $k_1 = 5.39$, $k_2 = 6.7$ and $\rho_{1000} = 8.0$, for cables or wires with reduced relaxation (class 2) $k_1 = 0.66$, $k_2 = 9.1$ and $\rho_{1000} = 2.5$, and for hot-rolled and modified rods (class 3) $k_1 = 1.98$, $k_2 = 8.0$ and $\rho_{1000} = 4.0$.

The prestress $\sigma_{init}$ is not specified in the input record. It is initialized automatically at the time instant when stress differs from zero.

The material model has one internal variable which has a meaning of cumulative prestress loss when equivalent time approach is employed; otherwise its meaning is a cumulative strain caused by relaxation.

Table 52: SteelRelaxMat material model - summary.

Description	SteelRelaxMat model for relaxation of prestressing reinforcement
Record Format	SteelRelaxMat d(rn) # E(rn) # reinfClass(in) # [ timeFactor(rn) #] charStrength(rn) # approach(in) # [ k1(rn) #] [ k2(rn) #] [ rho1000(rn) #] [ tolerance(rn) #] [ relRelaxBound(rn) #]
Parameters	- num material model number
	- d specific weight
	- E Young's modulus
	- reinfClass class of prestressing reinforcement (1, 2, 3)
	- timeFactor scaling factor transforming the actual time into appropriate units needed by the formulae of the eurocode. For analysis in days timeFactor = 1, for analysis in seconds timeFactor = 86,400.
	- charStrength characteristic strength of prestressing steel in appropriate units (not necessarily MPa)
	- approach 0 = approach according to Bazant and Yu, 1 = equivalent time approach according to Eurocode 2 and fib Model Code 2010
	- k1 possibility to overwrite default value given by the reinforcement class
	- k2 possibility to overwrite default value given by the reinforcement class
	- rho1000 possibility to overwrite default value given by the reinforcement class
	- tolerance applicable only for $approach = 0$; tolerance specifying the residual in the stress evaluation algorithm, default value is $10^{-6}$
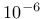	- relRelaxBound ratio of stress to characteristic strength under which the relaxation is zero (typically 0.4-0.5); default value is zero
Supported modes	1dMat