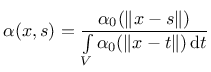| Description |
Nonlocal anisotropic elastoplastic model with isotropic damage |
| Record Format |
TrabBoneNL3d (in) #
d(rn) # eps0(rn) # nu0(rn) # mu0(rn) # expk(rn) # expl(rn) # m1(rn) # m2(rn) # rho(rn) #
sig0pos(rn) # sig0neg(rn) # chi0pos(rn) # chi0neg(rn) # tau0(rn) # plashardfactor(rn) # expplashard(rn) # expdam(rn) # critdam(rn) # m(rn) # R(rn) # |
| Parameters |
- material number |
| |
- d material density |
| |
- eps0 Young modulus (at zero porosity) |
| |
- nu0 Poisson ratio (at zero porosity) |
| |
- mu0 shear modulus (at zero porosity) |
| |
- m1 first eigenvalue of the fabric tensor |
| |
- m2 second eigenvalue of the fabric tensor |
| |
- rho volume fraction of the solid phase |
| |
- sig0pos yield stress in tension |
| |
- tau0 yield stress in shear |
| |
- chi0pos interaction coefficient in tension |
| |
- chi0neg interaction coefficient in compression |
| |
- plashardfactor hardening parameter |
| |
- expplashard exponent in the hardening law |
| |
- expdam exponent in the damage law |
| |
- critdam critical damage |
| |
- expk exponent  in the expression for elastic stiffness in the expression for elastic stiffness |
| |
- expl exponent  in the expression for elastic stiffness in the expression for elastic stiffness |
| |
- expq exponent  in the expression for tensor in the expression for tensor 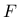 |
| |
- expp exponent  in the expression for tensor in the expression for tensor 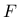 |
| |
- m over-nonlocal parameter |
| |
- R nonlocal interaction radius |
| Supported modes |
3dMat |