Isotropic damage model for tensile failure - Idm1

This isotropic damage model assumes that the stiffness degradation is isotropic, i.e., stiffness moduli corresponding to different directions decrease proportionally and independently of the loading direction. The damaged stiffness tensor is expressed as $D$$=(1-\omega)$$D$$_e$ where $\omega$ is a scalar damage variable and $D$$_e$ is the elastic stiffness tensor. The damage evolution law is postulated in an explicit form, relating the damage variable $\omega$ to the largest previously reached equivalent strain level, $\kappa$.

The equivalent strain, $\tilde\varepsilon$, is a scalar measure derived from the strain tensor. The choice of the specific expression for the equivalent strain affects the shape of the elastic domain in the strain space and plays a similar role to the choice of a yield condition in plasticity. The following definitions of equivalent strain are currently supported:

• Mazars (1984) definition based on norm of positive part of strain:

  $$\tilde\varepsilon=\sqrt{\displaystyle{\sum_{I=1}^{3}}\langle\varepsilon_I\rangle^2}$$ (69)

  
  
  where $\langle\varepsilon_I\rangle$ are positive parts of principal values of the strain tensor $\varepsilon$.
• Definitions derived from the Rankine criterion of maximum principal stress:
  

  $$\tilde\varepsilon = {\mbox{$\displaystyle\frac{1}{E}$}}\sqrt{\displaystyle{\sum_{I=1}^{3}}\langle\bar{\sigma}_I\rangle^2}$$ (70)

  $$\tilde\varepsilon = {\mbox{$\displaystyle\frac{1}{E}$}}\max_{I=1}^{3}\bar{\sigma}_I$$ (71)

  
  where $\bar{\sigma}_I$, $I=1,2,3$, are the principal values of the effective stress tensor $\bar{\mbox{\boldmath $\sigma$}} = \mbox{\boldmath $D$}_e:\mbox{\boldmath $\varepsilon$}$ and $\langle\bar{\sigma}_I\rangle$ are their positive parts.
• Energy norm scaled by Young's modulus to obtain a strain-like quantity:

  $$\tilde\varepsilon= \mbox{$\displaystyle\frac{1}{E}$} \sqrt{{\mbox{\boldmath$\varepsilon$}:\mbox{\boldmath$D$}_e:\mbox{\boldmath$\varepsilon$}}}$$ (72)

  
  

• Modified Mises definition, proposed by de Vree [26]:

  $$\tilde\varepsilon=\frac{(k-1)I_{1\varepsilon}}{2k(1-2\nu)} + \fra... ...(k-1)^2}{(1-2\nu)^2}I_{1\varepsilon}^2+\frac{12 k J_{2\varepsilon}}{(1+\nu)^2}}$$ (73)

  
  
  where
  $$I_{1\varepsilon} = \sum_{I=1}^3\varepsilon_I$$
  is the first strain invariant (trace of the strain tensor),
  $$J_{2\varepsilon} = \frac{1}{2}\sum_{I=1}^3 \varepsilon_I^2-\frac{1}{6}I_{1\varepsilon}^2$$
  is the second deviatoric strain invariant, and $k$ is a model parameter that corresponds to the ratio between the uniaxial compressive strength $f_c$ and uniaxial tensile strength $f_t$.
• Griffith definition with a solution on inclined elipsoidal inclusion. This definition handles materials in pure tension and also in compression, where tensile stresses usually appear on specifically oriented elipsoidal inclusion. The derivation of Griffith's criterion is summarized in [14]. In impementation, first check if Rankine criterion applies
  

  $$\tilde\varepsilon = {\mbox{$\displaystyle\frac{1}{E}$}}\max_{I=1}^{3}\bar{\sigma}_I$$ (74)

  
  and if not, use Griffith's solution with ordered principal stresses $\sigma_1>\sigma_3$. The optional parameter griff_n is by default 8 and represents the uniaxial compression/tensile strength ratio.

  
  

  $$\tilde\varepsilon = {\mbox{$\displaystyle\frac{1}{E}$}}\cdot{\mbox{$\displaystyle\frac{-(\sigma_1-\sigma_3)^2}{{\it griff\_n}(\sigma_1+\sigma_3)}$}}$$ (75)

  
  

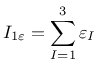
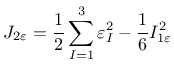
Note that all these definitions are based on the three-dimensional description of strain (and stress). If they are used in a reduced problem, the strain components that are not explicitly provided by the finite element approximation are computed from the underlying assumptions and used in the evaluation of equivalent strain. For instance, in a plane-stress analysis, the out-of-plane component of normal strain is calculated from the assumption of zero out-of-plane normal stress (using standard Hooke's law).

Since the growth of damage usually leads to softening and may induce localization of the dissipative process, attention should be paid to proper regularization. The most efficient approach is based on a nonlocal formulation; see Section 1.5.7. If the model is kept local, the damage law should be adjusted according to the element size, in the spirit of the crack-band approach. When done properly, this ensures a correct dissipation of energy in a localized band of cracking elements, corresponding to the fracture energy of the material. For various numerical studies, it may be useful to specify the parameters of the damage law directly, independently of the element size. One should be aware that in this case the model would exhibit pathological sensitivity to the size of finite elements if the mesh is changed.

The following damage laws are currently implemented:

• Cohesive crack with exponential softening postulates a relation between the normal stress $\sigma$ transmitted by the crack and the crack opening $w$ in the form
  $$\sigma = f_t\exp\left(-\frac{w}{w_f}\right)$$
  Here, $f_t$ is the tensile strength and $w_f$ is a parameter with the dimension of length (crack opening), which controls the ductility of the material. In fact, $w_f=G_f/f_t$ where $G_f$ is the mode-I fracture energy. In the context of the crack-band approach, the crack opening $w$ corresponds to the inelastic (cracking) strain $\varepsilon_c$ multiplied by the effective thickness $h$ of the crack band. The effective thickness $h$ is estimated by projecting the finite element onto the direction of the maximum principal strain (and stress) at the onset of damage. The inelastic strain $\varepsilon_c$ is the difference between the total strain $\varepsilon$ and the elastic strain $\sigma/E$. For the damage model we obtain
  $$\varepsilon_c = \varepsilon - \frac{\sigma}{E} = \varepsilon - (1-\omega)\varepsilon = \omega\varepsilon$$
  and thus $w=h\varepsilon_c=h\omega\varepsilon$. Substituting this into the cohesive law and combining with the stress-strain law for the damage model, we get a nonlinear equation
  $$(1-\omega)E\varepsilon = f_t\exp\left(-\frac{h\omega\varepsilon}{w_f}\right)$$
  For a given strain $\varepsilon$, the corresponding damage variable $\omega$ can be solved from this equation by Newton iterations. It can be shown that the solution exists and is unique for every $\varepsilon\ge\varepsilon_0$ provided that the element size $h$ does not exceed the limit size $h_{max}=w_f/\varepsilon_0$. For larger elements, a local snapback in the stress-strain diagram would occur, which is not admissible. In terms of the material properties, $h_{max}$ can be expressed as $EG_f/f_t^2$, which is related to Irwin's characteristic length.

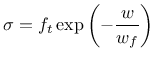
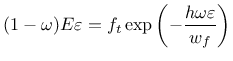
  The derivation has been performed for monotonic loading and uniaxial tension. Under general conditions, $\varepsilon$ is replaced by the internal variable $\kappa$, which represents the maximum previously reached level of equivalent strain.

  In the list of input variables, the tensile strength $f_t$ is not specified directly but through the corresponding strain at peak stress, $\varepsilon_0=f_t/E$, denoted by keyword e0. Another input parameter is the characteristic crack opening $w_f$, denoted by keyword wf.

  Derivative can be expressed explicitly

  $$\frac{\partial\omega}{\partial\varepsilon} = - \frac{(\omega \var... ... \frac{\omega \varepsilon}{\varepsilon_f}\right ) - \varepsilon_0 \varepsilon}$$

• Cohesive crack with linear softening is based on the same correspondence between crack opening and inelastic strain, but the cohesive law is assumed to have a simpler linear form
  $$\sigma = f_t\left(1-\frac{w}{w_f}\right)$$
  The relation between damage and strain can then be derived from the cohesive law and substituing $w=h \omega \varepsilon$
  $$\sigma = (1-\omega)E\varepsilon = f_t\left(1-\frac{h \omega \varepsilon}{w_f}\right),$$
  which leads to explicit evaluation of the damage variable
  $$\omega=\frac{1-\displaystyle\frac{\varepsilon_0}{\varepsilon}}{1-\displaystyle\frac{h\varepsilon_0}{w_f}}$$
  and no iteration is needed. Parameter $w_f$, denoted again by keyword wf, has now the meaning of crack opening at complete failure (zero cohesive stress) and is related to fracture energy by a modified formula $w_f=2G_f/f_t$. The expression for maximum element size, $h_{max}=w_f/\varepsilon_0$, remains the same as for cohesive law with exponential softening, but in terms of the material properties it is now translated as $h_{max}=2EG_f/f_t^2$. The derivative with respect to $\varepsilon$ yields
  $$\frac{\partial\omega}{\partial\varepsilon} = \frac{\varepsilon_0}{\varepsilon^2 \left ( 1-\frac{h \varepsilon_0}{w_f}\right )}$$

• Cohesive crack with bilinear softening is implemented in an approximate fashion and gives for different mesh sizes the same total dissipation but different shapes of the softening diagram. Instead of properly transforming the crack opening into inelastic strain, the current implementation deals with a stress-strain diagram adjusted such that the areas marked in the right part of Fig. 6 are equal to the fracture energies $G_f$ and $G_{ft}$ divided by the element size. The third parameter defining the law is the strain $\varepsilon$$_k$ at which the softening diagram changes slope. Since this strain is considered as fixed, the corresponding stress $\sigma_k$ depends on the element size and for small elements gets close to the tensile strength (the diagram then gets close to linear softening with fracture energy $G_{ft}$).
• Linear softening stress-strain law works directly with strain and does not make any adjustment for the element size. The specified parameters $\varepsilon_0$ and $\varepsilon _f$, denoted by keywords e0 and ef, have the meaning of (equivalent) strain at peak stress and at complete failure. The linear relation between stress and strain on the softening branch is obtained with the damage law
  $$\omega =\frac{\varepsilon_f}{\varepsilon_f-\varepsilon_0}\left(1-\frac{\varepsilon_0}{\varepsilon}\right)$$
  Again, to cover general conditions, $\varepsilon$ is replaced by $\kappa$.
  $$\frac{\partial\omega}{\partial\varepsilon} = \frac{\varepsilon_0 \varepsilon_f}{\varepsilon^2 ( \varepsilon_f - \varepsilon_0 )}$$

• Exponential softening stress-strain law also uses two parameters $\varepsilon_0$ and $\varepsilon _f$, denoted by keywords e0 and ef, but leads to a modified dependence of damage on strain:
  $$\omega =1-\frac{\varepsilon_0}{\varepsilon}\exp\left(-\frac{\varepsilon-\varepsilon_0}{\varepsilon_f-\varepsilon_0}\right)$$
  $$\frac{\partial\omega}{\partial\varepsilon} = \left[ \frac{1}{\var... ... \left (\frac{\varepsilon_0-\varepsilon}{\varepsilon_f-\varepsilon_0} \right )$$

• Mazars stress-strain law uses three parameters, $\varepsilon_0$, $A_t$ and $B_t$, denoted by keywords e0, At and Bt, and the dependence of damage on strain is given by
  $$\omega =1-\frac{(1-A_t)\varepsilon_0}{\varepsilon}-A_t\exp\left(B_t(\varepsilon-\varepsilon_0)\right)$$

• Smooth exponential stress-strain law uses two parameters, $\varepsilon_0$ and $M_d$, denoted by keywords e0 and md, and the dependence of damage on strain is given by
  $$\omega = 1-\exp\left(-\left(\frac{\varepsilon}{\varepsilon_0}\right)^{M_d}\right)$$
  This leads to a stress-strain curve that immediately deviates from linearity (has no elastic part) and smoothly changes from hardening to softening, with tensile strength
  $$f_t = E\varepsilon_0\left({\rm e}M_d\right)^{-1/M_d}$$

• Extended smooth stress-strain law is a special formulation used by Grassl and Jirásek [10]. The damage law has a rather complicated form:

  $$\omega = \left \{ \begin{array}{ll} 1-\exp\left(-\displaystyle\fr... ... & \mbox{if $\mbox{\boldmath$\varepsilon$}> \varepsilon_1$} \end{array} \right.$$ (76)

  
  
  The primary model parameters are the uniaxial tensile strength $f_{\rm t}$, the strain at peak stress (under uniaxial tension) $\varepsilon_{\rm p}$, and additional parameters $\varepsilon_1$, $\varepsilon_2$ and $n$, which control the post-peak part of the stress-strain law. In the input record, they are denoted by keywords ft, ep, e1, e2, nd. Other parameters that appear in (76) can be derived from the condition of zero slope of the stress-strain curve at $\kappa=\varepsilon_{\rm p}$ and from the conditions of stress and stiffness continuity at $\kappa=\varepsilon_1$:
  

  $$m = \frac{1}{\ln(E\varepsilon_{\rm p}/f_{\rm t})}$$ (77)

  $$\varepsilon_{\rm f} = \frac{\varepsilon_1}{\left(\varepsilon_1/\varepsilon_{\rm p}\right)^m -1}$$ (78)

  $$\varepsilon_3 = \varepsilon_1\exp\left(-\frac{1}{m}\left(\frac{\varepsilon_1}{\varepsilon_p}\right)^m\right)$$ (79)

  
  

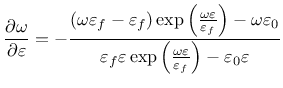
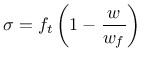
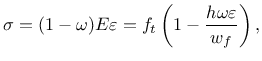
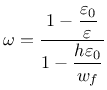
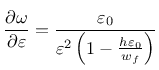
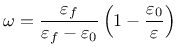
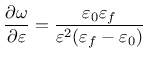
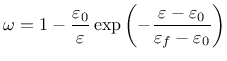
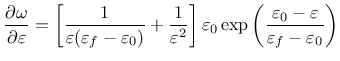
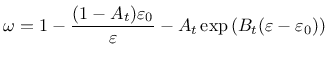
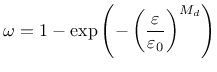
Note that parameter damlaw determines which type of damage law should be used, but the adjustment for element size is done only if parameter wf is specified for damlaw=0 or damlaw=1. For other values of damlaw, or if parameter ef is specified instead of wf, the stress-strain curve does not depend on element size and the model would exhibit pathological sensitivity to the mesh size. These cases are intended to be used in combination with a nonlocal formulation. An alternative formulation uses fracture energy to determine fracturing strain.

The model parameters are summarized in Tab. 23. Figure 6 shows three modes of a softening law with corresponding variables.

Figure: Implemented stress-strain diagrams for isotropic damage material. Fracturing strain $\varepsilon _f$ and crack opening at zero stress $w_f$ are interrelated through effective thickness $h$ of the crack band. Note that exponential softening approach based on an exponential cohesive law is not exactly equivalent to the approach based on an exponential softening branch of the stress-strain diagram; see the detailed discussion of the damage laws.

Table 23: Isotropic damage model for tensile failure - summary.

Description

Isotropic damage model for concrete in tension

Record Format

Idm1 (in) # d(rn) # E(rn) # n(rn) # [tAlpha(rn) #] [equivstraintype(in) #] [k(rn) #] [damlaw(in) #] e0(rn) # [wf(rn) #] [ef(rn) #] [ek(rn) #] [wk(rn) #] [sk(rn) #] [wkwf(rn) #] [skft(rn) #] [gf(rn) #] [gft(rn) #] [At(rn) #] [Bt(rn) #] [md(rn) #] [ft(rn) #] [ep(rn) #] [e1(rn) #] [e2(rn) #] [nd(rn) #] [maxOmega(rn) #] [checkSnapBack(rn) #]

Parameters

- material number

- d material density

- E Young's modulus

- n Poisson's ratio

- tAlpha thermal expansion coefficient

- equivstraintype allows to choose from different definitions of equivalent strain:

0 -	default = Mazars, eq. (69)
1 -	smooth Rankine, eq.  (70)
2 -	scaled energy norm, eq. (72)
3 -	modified Mises, eq. (73)
4 -	standard Rankine, eq. (71)
5 -	elastic energy based on positive stress
6 -	elastic energy based on positive strain
7 -	Griffith criterion eq. (75)

- k ratio between uniaxial compressive and tensile strength, needed only if equivstraintype=3, default value 1

- damlaw allows to choose from different damage laws:

0 -	exponential softening (default) with parameters e0 and wf $\vert$ ef $\vert$ gf
1 -	linear softening with parameters e0 and wf $\vert$ ef $\vert$ gf
2 -	bilinear softening with (e0, gf, gft, ek) $\vert$ (e0, wk, sk, wf) $\vert$ (e0, wkwf, skft, wf) $\vert$ (e0, gf, gft, wk)
3 -	Hordijk softening (not implemented yet)
4 -	Mazars damage law with parameters At and Bt
5 -	smooth stress-strain curve with parameters e0 and md
6 -	disable damage (dummy linear elastic material)
7 -	extended smooth damage law (76) with parameters ft, ep, e1, e2, nd

- e0 strain at peak stress (for damage laws 0,1,2,3), limit elastic strain (for damage law 4), characteristic strain (for damage law 5)

- wf parameter controling ductility, has the meaning of crack opening (for damage laws 0 and 1)

- ef parameter controling ductility, has the meaning of strain (for damage laws 0 and 1)

- ek strain at knee point in bilinear softening type (for damage law 2)

- wk crack opening at knee point in bilinear softening type (for damage law 2)

- sk stress at knee point in bilinear softening type (for damage law 2)

- wkwf ratio of wk/wf $<0,1>$ in bilinear softening type (for damage law 2)

- skft ratio of sk/ft $<0,1>$ in bilinear softening type (for damage law 2)

- gf fracture energy (for damage laws 0-2)

- gft total fracture energy (for damage law 2)

- At parameter of Mazars damage law, used only by law 4

- Bt parameter of Mazars damage law, used only by law 4

- md exponent used only by damage law 5, default value 1

- ft tensile strength, used only by damage law 7

- ep strain at peak stress, used only by damage law 7

- e1 parameter used only by damage law 7

- e2 parameter used only by damage law 7

- nd exponent used only by damage law 7

- griff_n uniaxial compression/tensile ratio for Griffith's criterion

- maxOmega maximum damage, used for convergence improvement (its value is between 0 and 0.999999 (default), and it affects only the secant stiffness but not the stress)

- checkSnapBack parameter for snap back checking, 0 no check, 1 check (default)

Supported modes

3dMat, PlaneStress, PlaneStrain, 1dMat

Features

Adaptivity support