In the tension mode, the exponential softening law is assumed (see fig.(3)). The yield function has the following form
where the yield value  is defined as
is defined as
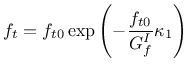 |
(58) |
Figure:
Tensile behavior of proposed model ( MPa,
MPa,
 N/mm)
N/mm)
|
|
The  represents tensile strength of joint or interface; and
represents tensile strength of joint or interface; and  is mode-I fracture energy. For the tension mode, the associated flow hypothesis is assumed.
is mode-I fracture energy. For the tension mode, the associated flow hypothesis is assumed.
Borek Patzak
2019-03-19