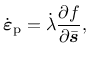The small-strain version of hardening Mises plasticity can be combined with isotropic damage.
The basic equations include the additive decomposition of strain into elastic and plastic parts,
the stress strain law
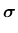 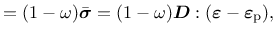 |
(39) |
the definition of the yield function in terms of the effective stress,
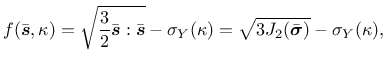 |
(40) |
the incremental definition of cumulative plastic strain
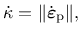 |
(41) |
the linear hardening law
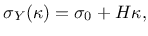 |
(42) |
the evolution law for the plastic strain
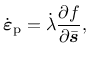 |
(43) |
the loading-unloading conditions
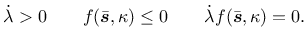 |
(44) |
and the damage law
 e e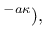 |
(45) |
In the equations above,
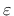 is the strain tensor,
is the strain tensor,
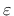
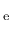 is the elastic strain tensor,
is the elastic strain tensor,
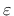
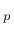 is the plastic strain tensor,
is the plastic strain tensor,
 is the elastic stiffness tensor,
is the elastic stiffness tensor,
 is the nominal stress tensor,
is the nominal stress tensor,
 is the effective stress tensor,
is the effective stress tensor,
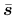 is the effective deviatoric stress tensor,
is the effective deviatoric stress tensor,  is the magnitude of stress at yielding under uniaxial tension (or compression),
is the magnitude of stress at yielding under uniaxial tension (or compression),  is the cumulated plastic strain,
is the cumulated plastic strain,  is the hardening modulus,
is the hardening modulus,  is the plastic multiplier,
is the plastic multiplier,  is the damage variable,
is the damage variable,  is critical damage and
is critical damage and  is a positive dimensionless parameter.
is a positive dimensionless parameter.
Borek Patzak
2019-03-19